Researchers have successfully demonstrated that the theoretically optimal scaling for magic state distillation, a crucial process in fault-tolerant quantum computing, is achievable for qubits. This advancement improves upon previous results, reaching a scaling exponent of precisely zero. The findings, published in Nature Physics on November 12, 2025, address a significant open problem that has persisted in quantum computing for years.
Adam Wills, a Ph.D. student at the Massachusetts Institute of Technology (MIT) and lead author of the study, emphasized the importance of this achievement, stating, “Broadly, I think that building quantum computers is a wonderful and inspiring goal. However, it is an extremely challenging goal.” The primary hurdle in developing functional quantum computers lies in managing noise, as qubits are highly sensitive to environmental disturbances and require robust error-correcting codes for protection.
Error correction alone proves insufficient, as the codes that safeguard qubits inherently support only specific operations known as Clifford gates. These operations cannot provide a quantum advantage independently. To implement necessary non-Clifford operations in a fault-tolerant manner has remained a major bottleneck in the field.
Magic state distillation, introduced by Bravyi and Kitaev in 2005, offers a solution by enabling these operations through specially prepared quantum states. However, the process has been resource-intensive, with overhead—the number of noisy input states required to produce a high-quality output state—growing as error rates decrease.
The Role of Magic States in Quantum Computation
In the context of quantum computing, “magic” represents a quantifiable resource. According to Bravyi and Kitaev’s foundational work, universal quantum computation is achievable when Clifford operations are supplemented with unique quantum states called magic states. These states exist outside the realm of stabilizer states, where classical computers can compete, and provide quantum contextuality, enhancing the capabilities of quantum systems.
Magic states can be utilized through a process known as gate teleportation to execute essential non-Clifford gates for universal quantum computation. For instance, a T gate can be implemented by consuming one magic state alongside Clifford operations and measurements. Nevertheless, researchers typically generate noisy magic states with error rates around 10^-3, while achieving quantum advantage necessitates reducing these rates to approximately 10^-7. For large-scale algorithms, error rates as low as 10^-15 or lower are essential.
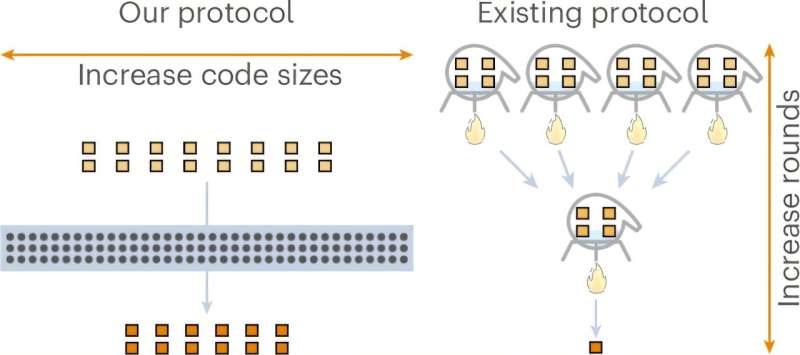
This is where the optimization of magic state distillation comes into play. The efficiency of this process is measured by its overhead—specifically, the ratio of input magic states to output magic states needed to reach a target error rate. Historically, this overhead has increased as the target error rate decreases, characterized by a scaling exponent, denoted as γ (gamma). A lower γ indicates more efficient distillation, with achieving γ = 0 signifying constant overhead regardless of the required purity of the final states.
Recent progress has been made in reducing this scaling. In 2017, Hastings and Haah achieved γ ≈ 0.678. In 2018, Krishna and Tillich approached γ = 0, but only for increasingly larger quantum systems, lacking a clear pathway to practical qubit systems. Wills and his team have now established that γ = 0 is feasible.
Innovative Discoveries in Distillation Techniques
Wills explained that the discovery unfolded in two stages over several months. The first breakthrough was the realization that algebraic geometry codes would be particularly beneficial for this issue. Earlier attempts employed various classical error-correcting codes, such as the Reed-Muller codes used by Hastings and Haah, which could not reduce overhead below γ ≈ 0.678.
The second significant finding emerged from studying a textbook by Dan Gottesman, where the team discovered that they could represent their qudits—quantum systems with 1,024 levels—as sets of qubits. This conversion allowed them to adapt their constant-overhead protocol from qudits to qubits. Consequently, magic states originally based on 10 qubits could be transformed into standard single-qubit and three-qubit magic states with minimal overhead loss.
With these two innovations, the team demonstrated that constant overhead (γ = 0) is achievable for qubit systems, which marks a significant theoretical advancement in the field.
The implications of this work establish a fundamental theoretical limit; no better asymptotic scaling for magic state distillation overhead is possible. Nevertheless, Wills noted the gap between theoretical advancements and practical implementation. While the γ = 0 scaling is theoretically optimal, the actual resource demands may require significantly more physical qubits than are currently available in near-term quantum computers.
Wills highlighted the importance of establishing these theoretical foundations for advancing fault-tolerant quantum computing, stating, “Developing a solid theory of quantum magic is incredibly important for pushing fault-tolerance further in all regimes, because we know it is essential for universal quantum computation.”
The research team is currently exploring extensions of their work, including Wills’s recent investigations into transversally addressable gates. Future research will focus on optimizing constant factors, exploring quantum LDPC code variants, and identifying optimal qudit-to-qubit conversions, all of which hold promise for the future of quantum computing.