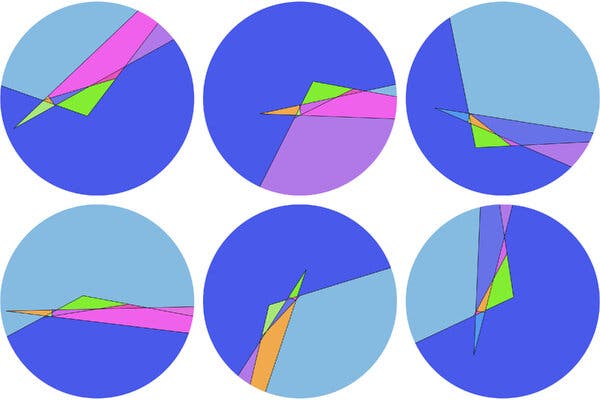
A recent academic paper by mathematicians Neil J.A. Sloane and David O.H. Cutler delves into the intriguing challenge of cutting an infinitely large pancake into as many pieces as possible. This research revisits a well-known mathematical puzzle known as the Lazy Caterer’s Problem, introducing innovative approaches to a classic conundrum.
The study, which was posted online, explores the complexities of dividing an infinite pancake that spreads endlessly in all directions. The authors employed both a straight knife and various uniquely shaped knives to determine the optimal cutting strategies. Sloane, the founder of the On-Line Encyclopedia of Integer Sequences, noted the importance of finding the “sweet spot” in applying these cutting techniques.
Background on the Lazy Caterer’s Problem
The Lazy Caterer’s Problem, first discussed in the 1980s, examines how many pieces a pancake can be divided into with a given number of straight cuts. The problem gained popularity through its inclusion in the influential book Concrete Mathematics: A Foundation for Computer Science, which was based on a Stanford course of the same name. In this context, “concrete mathematics” serves as a counterpoint to the increasingly abstract approaches emerging in the field.
Sloane and Cutler engaged in extensive trial and error to navigate the intricate task of maximizing the number of pieces from the infinite pancake. Their findings not only contribute to the understanding of mathematical principles but also highlight the creativity involved in problem-solving within the field.
The research presents a fresh perspective on a classic topic, reminding us that mathematics can be both challenging and engaging. As Sloane and Cutler continue to explore this fascinating area, their work could inspire further studies and discussions in mathematical circles.